Wave prediction

Timelapse photography of body of water - Picture By Thierry Meier

Large ocean waves and the consequent wave-induced motions of a floating facility are of great concern as they pose a safety hazard to personnel and can lead to operational downtime. It is therefore highly desirable to have real-time forward-prediction capability (up to several wave periods) to improve the safety and efficiency of a wide range of maritime activities, especially when these are close to their perceived operational limits. Accurate wave prediction can provide a decision-making tool to identify the optimal time for conducting crucial activities such as maintenance.

Real-time prediction of phase-resolved surface waves is challenging due to the complexity of real ocean conditions. To at least partially overcome the difficulties of predicting moderate directional spreading waves, we adopt a machine-learning approach, specifically one based on neural networks. The focus of this simulation study is to use up-wave data to forecast wave-surface elevations at a specific location down-wave. Figure 1 shows a schematic of the set-up for our simulation experiment, which uses four wave buoys, three up-wave buoys and one down-wave buoy. The distance between the up-wave and down-wave buoys is set at twice the peak wavelength, 2λ_𝘱 (λ_𝘱 = 225m, which we have control over), along the mean wave direction (θ̅ = 0°). The angle subtended between the two extreme up-wave buoys and the down-wave buoy is 2θ_b = 20°.

Figure 1: Schematic of the experimental set-up: three up-wave buoys B₁ and B₂ (red dots) and B₃ (yellow dot),
and one down-wave buoy P (blue dot).
The prediction location P is 2λ𝘱 down-wave, along the mean wave direction (θ̅ = 0°).

We adopt the same sea state as in the theoretical analysis by Hlophe et al. (2022): The waves are generated based on synthetic linear, short-crested waves with the Joint North Sea Wave Project (JONSWAP) spectrum (Hasselmann et al., 1973); see Chen et al. (2023d) for further details.

An artificial neural network is a machine-learning model inspired by biological nervous systems. It is a universal function approximator and therefore very flexible (Zhou, 2020). The goal of an artificial neural network is to learn a function that maps an input x to a predicted output y in such a way that the prediction is optimal in some sense (usually in such a way that the expected squared error between the prediction and the underlying true value is minimised).

For surface-wave prediction in this study, the time history of surface-wave elevations at up-wave locations B₁ and B₂ are used to predict the surface-wave elevation at the down-wave location P using a neural network. Initially, we consider a pair of up-wave buoys: η_B1(t) and η_B2(t) are the surface-wave elevations at up-wave locations at n timesteps, t = t₁, t₂, ..., t_n. Further, let η̃_P(t) be the predicted surface-wave elevation at the down-wave location at m timesteps, t = t₁, t₂, ..., t_m. A schematic of a neural network that takes as input data from the wave buoys at the two up-wave locations is illustrated in Figure 2. The neural network comprises an input layer, two hidden layers, and an output layer.

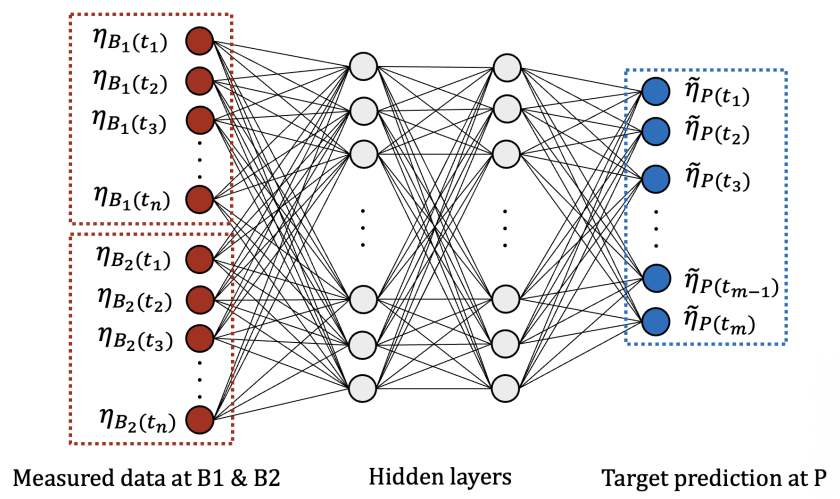
Figure 2: Schematic of a neural network designed for surface-wave prediction. The neural network approximates the true relationship between the input at the up-wave locations, B₁ and B₂ (highlighted in red box), and the output at the down-wave location, P (highlighted in the blue box).

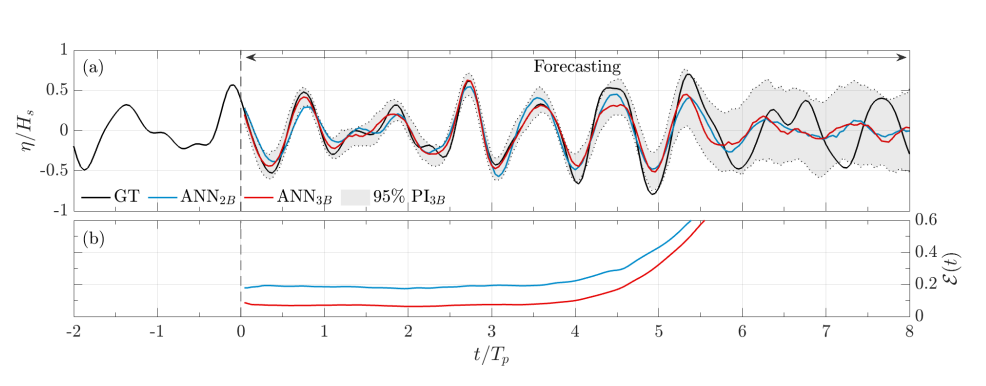
Figure 3: (a) Wave prediction on a single test dataset at distance 2λ_p down-wave, where the black line is the ground truth, GT; the blue line is the prediction using two wave buoys, ANN_2B ; the red line and the shaded area are the predictions using three wave buoys, ANN_3B , and the shading is the 95% prediction interval (PI_3B) of ANN_3B . (b) The average error, ε(t), evaluated from 300 test datasets. T_p is the wave period and H_s is the so-called "significant wave height."

We train two neural networks on simulated data, one that uses two wave buoys for forecasting and one that uses all three. We then test the neural networks on test datasets (datasets not used for training). In Figure 3, we plot the forecasts from the two neural networks on a test dataset and an average error from 300 test datasets. Both neural networks perform well, but clearly the prediction is more accurate when using three up-wave buoys instead of two. Specifically, the three-buoy model can achieve accurate prediction (average error smaller than 0.1 units) for up to four wave time periods (4T_p) ahead. More complex neural network architectures and applications to field data are currently being investigated.

This is a joint work with Jialun Chen, Wenhua Zhao, Paul Taylor, and Ian Milne from the University of Western Australia. For more information on this work see Chen et al. (2023a), Chen et al. (2023b), and Chen et al. (2023c).

Chen, J., Hlophe, T., Zhao, W., Milne, I. A., Gunawan, D., Kurniawan, A., Wolgamot, H., Taylor, P. H., and Orszaghova, J. (2023a). Comparison of physics-based and machine learning methods for phase-resolved prediction of waves measured in the field. In Proceedings of the European Wave and Tidal Energy Conference, volume 15, pages 1–9.

Chen, J., Milne, I., Taylor, P. H., Gunawan, D., and Zhao, W. (2023b). Forward prediction of surface wave elevations and motions of offshore floating structures using a data-driven model. Ocean Engineering, 281:114680.

Chen, J., Milne, I. A., Gunawan, D., Taylor, P. H., and Zhao, W. (2023c). Weakly nonlinear surface wave prediction using a data-driven method with the help of physical understanding. Journal of Offshore Mechanics and Arctic Engineering, 146(4):041201.

Chen, J., Taylor, P. H., Milne, I. A., Gunawan, D., and Zhao, W. (2023d). Wave-by-wave prediction for spread seas using a machine learning model with physical understanding. Ocean Engineering, 285:115450.

Hasselmann, K., Barnett, T. P., Bouws, E., Carlson, H., Cartwright, D. E., Enke, K., Ewing, J., Gienapp, A., Hasselmann, D., Kruseman, P., et al. (1973). Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deutsche hydrographische Zeitschrift, 8:1–95.

Hlophe, T., Wolgamot, H., Taylor, P. H., Kurniawan, A., Orszaghova, J., and Draper, S. (2022). Wave-by-wave prediction in weakly nonlinear and narrowly spread seas using fixed-point surface-elevation time histories. Applied Ocean Research, 122:103112.

Zhou, D.-X. (2020). Universality of deep Convolutional Neural Networks. Applied and Computational Harmonic Analysis, 48(2):787–794.

Authored by David Gunawan, 2024