Multi-Resolution Spatial Model (MRSM) Details
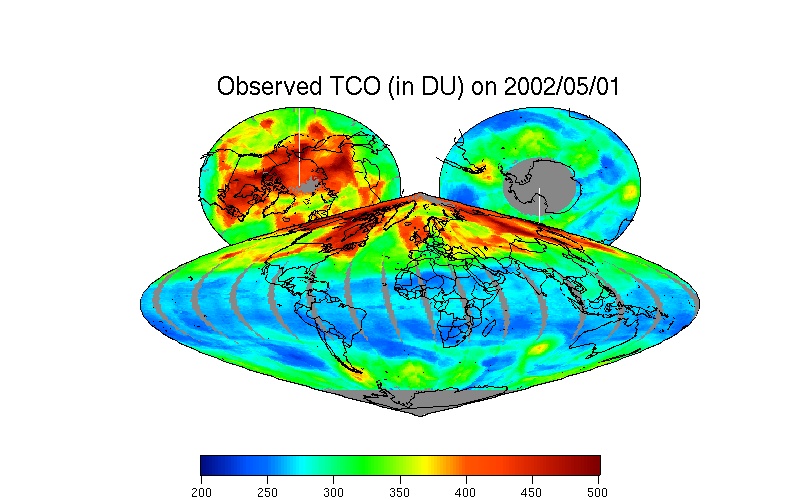
Remote sampling via satellites allows environmental data such as total column ozone (TCO) to be sampled at a given frequency and at a fine spatial resolution over the entire globe, yielding massive space-time data. However, data quality and availability are not uniform. For example, TCO data are sparse at some low-latitude locations because of the limitations in the satellite orbits and are unavailable near the poles during the polar winter because no sunlight is available. Additionally, for engineering and physical reasons there are inevitable sources of noise. The Multi-Resolution Spatial Model (MRSM) is a fast and effective tool to analyze and estimate massive amounts of spatial environmental data and to interpolate the missing values. The MRSM is based on trend-fitting, variance-covariance inference, and the change-of-resolution Kalman filter. The application of the MRSM to TCO shown on this website should be thought of as an illustration of what can be achieved more generally. Related references are Huang and Cressie (2001), Huang, Cressie, and Gabrosek (2002), Johannesson (2003), Johannesson and Cressie (2004), and Johannesson, Cressie, and Huang (2007).
The challenge of modeling massive spatial or spatio-temporal data stems not only from computational issues due to the sheer volume of data, but also from the scale of the spatial domain itself. When the spatial domain is large, one can expect a heterogeneous pattern of spatial variation in the data, giving rise to nonstationary spatial dependence. For example, the spatial variation in the TCO data observed in the polar region could be quite different from that observed near the equator. Therefore, detecting and fitting a large-scale spatial trend is often the first step in a comprehensive spatial analysis. A common spatial-analysis approach is to represent the large-scale feature or the trend in the spatial process of interest using a deterministic or parametric surface, and to capture the small-scale variation of the process using a stochastic random field (e.g., Cressie, 1993). For the TCO example, the large-scale spatial trend is associated with the coarser resolution features, although the data are sampled at a fine spatial resolution. To benefit from this property, the MRSM uses a sequential aggregation of the massive fine-resolution data to coarser and coarser resolutions, from which the trend is fitted to the more manageable coarser-resolution aggregated data. In Johannesson and Cressie (2004), data fidelity and trend-surface consistency measures are suggested for comparing trend surfaces fitted using aggregated data at various resolutions. In addition, measures are introduced that quantify and qualify the spatial variation in the detrended data, that is, in the spatial residuals.
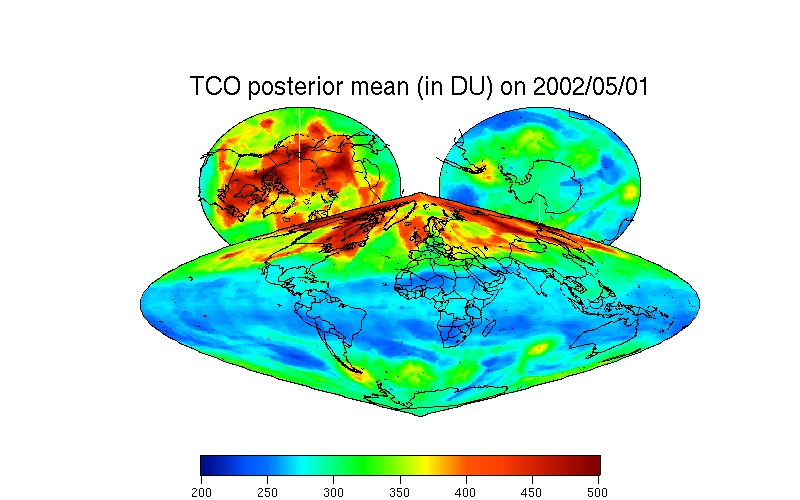
After detrending the data, the MRSM uses a resolution-ordered Kalman filter to calculate the posterior mean of the TCO (see Huang, Cressie, and Gabrosek, 2002). Another method to process the spatial data is kriging (e.g., Cressie, 1993). However, since the computational cost of kriging is cubic in the number of data, using kriging in massive-data situations ranges from being very difficult to impossible. Based on the multi-resolution framework, the computational complexity can be a factor 10-8 less than that of kriging. That is, the MRSM yields speed-ups by a factor of 100 million.
The MRSM was originally introduced for modeling massive spatial data based on a more general tree-structured multi-scale model (Chou et al., 1994). The MRSM uses a tree-structured recursive partition of the spatial domain to yield grids (images) at multiple resolutions. The spatial dependence in the process model is obtained from a coarse-to-fine-resolution model that describes the stochastic evolution from the parent cells at one resolution to the children cells at the next (finer) resolution. The attractiveness of the MRSM lies in the fact that it is both able to capture nonstationary spatial dependence through the specification of coarse-to-fine-resolution-process variance parameters and it is able to process massive amounts of data due to its tree-structured nature.
Before the multi-resolution Kalman filtering can be implemented, the variance-covariance structure must be estimated. To do this, assumptions are made about the variance-covariance structure of the parent-to-children process errors (Chou et al., 1994; Kolaczyk and Huang, 2001; Johannesson and Cressie, 2004). Estimation of unknown parameters is then carried out via resolution-specific-restricted-likelihood (RESREL) methods found in Johannesson and Cressie (2004). Alternatively, the variance-covariance structure could be estimated via maximum likelihood (e.g., Kolaczyk and Huang, 2001) or nonparametrically (Huang et al., 2002).
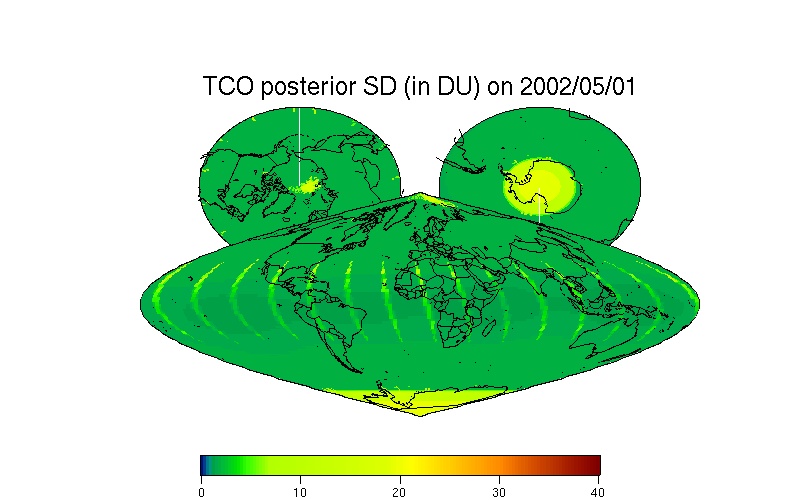
This website shows the performance of the MRSM model by processing the TOMS TCO data from May 1, 2002 to Dec. 31, 2002 (ozone-hole splitting event) and more recently. During this period, the Antarctic region experienced an unusual stratospheric warming event and the ozone hole unexpectedly split into two. The MRSM method interpolates all the missing data, and therefore it restores statistically the 2002 ozone-hole splitting event based on respective daily TCO observations. This spatial predictor (or smoother) is accompanied by a measure of the predictor's uncertainty; from inspection of the uncertainty (SD) map, the uneven spatial distribution of the TCO data is apparent.
Overall, the MRSM is one of the fastest methods of spatial prediction of in situ massive spatial data, it is statistically optimal (minimizes mean squared prediction error), and it is accompanied with a measure of uncertainty for each predicted value.