Banerjee, S., Carlin, B. P., and Gelfand, A. E. (2004). Hierarchical Modeling and Analysis for Spatial Data. Chapman & Hall/CRC Press, Boca Raton, FL.
Besag, J. (1974). Spatial interaction and the statistical analysis of lattice systems, Journal of the Royal Statistical Society, Series B, 36, 192-236.
Chiles, J.-P. and Delfiner, P., (1999). Geostatistics: Modelling Spatial Uncertainty. Wiley, New York, NY.
Connor, B. J., Bosch, H., Toon, G., Sen, B., Miller, C. and Crisp, D. (2008). Orbiting Carbon Observatory: Inverse method and prospective error analysis. Journal of Geophysical Research: Atmospheres, 113, 1-14.
Cressie, N. (1993). Statistics for Spatial Data (revised edition). Wiley, New York, NY.
Cressie, N. (2018). Mission CO2ntrol: A statistical scientist’s role in remote sensing of atmospheric carbon dioxide, (with discussion). Journal of the American Statistical Association, 113, 152-181.
Cressie, N. and Johannesson, G. (2008). Fixed rank kriging for very large spatial data sets. Journal of the Royal Statistical Society, Series B, 70, 209-226.
Cressie, N., Shi, T., and Kang, E. L. (2010). Fixed rank filtering for spatio-temporal data. Journal of Computational and Graphical Statistics, 19, 724-745.
Cressie, N. and Wang, R. (2013), Statistical properties of the state obtained by solving a nonlinear multivariate inverse problem. Applied Stochastic Models in Business and Industry, 29, 424-438.
Cressie, N. and Wikle, C. K. (2011). Statistics for Spatio-Temporal Data. Wiley, Hoboken, NJ.
Crisp, D., Fisher, B. M., O'Dell, C., Frankenberg, C., Basilio, R., Bosch, H., Brown, L. R., Castano, R., Connor, B., Deutscher, N. M., Eldering, A., Griffith, D., Gunson, M., Kuze, A., Mandrake, L., McDuffie, J., Messerschmidt, J., Miller, C. E., Morino, I., Natraj, V., Notholt, J., O'Brien, D. M., Oyafuso, F., Polonsky, I., Robinson, J., Salawitch, R., Sherlock, V., Smyth, M., Suto, H., Taylor, T. E., Thompson, D. R., Wennberg, P. O., Wunch, D. and Yung, Y. L. (2012). The ACOS CO2 retrieval algorithm - Part II: Global XCO2 data characterization. Atmospheric Measurement Techniques, 5, 687-707.
Doicu, A., Trautmann, T., and Schreier, F. (2010). Numerical Regularization for Atmospheric Inverse Problems. Springer, Berlin.
O'Dell, C. W., Connor, B., Bosch, H., O'Brien, D., Frankenberg, C., Castano, R., Christi, M., Eldering, D., Fisher, B., Gunson, M., McDuffie, J., Miller, C. E., Natraj, V., Oyafuso, F., Polonsky, I., Smyth, M., Taylor, T., Toon, G. C., Wennberg, P. O. and Wunch, D. (2012). The ACOS CO2 retrieval algorithm - Part 1: Description and validation against synthetic observations. Atmospheric Measurement Techniques, 5, 99-121.
Kang, E. and Cressie, N. (2011). Bayesian Inference for the Spatial Random Effects Model. Journal of the American Statistical Association, 106, 972-983.
Katzfuss, M. and Cressie, N. (2011). Spatio-temporal smoothing and EM estimation for massive remote-sensing data sets. Journal of Time Series Analysis, 32, 430-446.
Le, N. D., and Zidek, J. V. (2006). Statistical Analysis of Environmental Space-Time Processes. Springer, New York, NY.
Lindgren, F., Rue, H., and Lindstrom, J. (2011). An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach (with discussion). Journal of the Royal Statistical Society, Series B, 73, 423-498.
Nguyen H., Cressie N., Braverman A. (2012). Spatial statistical data fusion for remote sensing applications. Journal of the American Statistical Association, 107, 1004-1018.
Ripley, B. D. (1981). Spatial Statistics. Wiley, New York, NY.
Rodgers, C. D. (2000). Inverse Methods for Atmospheric Sounding: Theory and Practice. World Scientific, Singapore.
Rothman, L. S., Gordon, I. E., Babikov, Y., Barbe, A., Chris Benner, D., Bernath, P. F., Birk, M., Bizzocchi, L., Boudon, V., Brown, L. R., Campargue, A., Chance, K., Cohen, E. A., Coudert, L. H., Devi, V. M., Drouin, B. J., Fayt, A., Flaud, J. M., Gamache, R. R., Harrison, J. J., Hartmann, J. M., Hill, C., Hodges, J. T., Jacquemart, D., Jolly, A., Lamouroux, J., Le Roy, R. J., Li, G., Long, D. A., Lyulin, O. M., Mackie, C. J., Massie, S. T., Mikhailenko, S. , Muller, H. , Naumenko, O. V., Nikitin, A. V., Orphal, J., Perevalov, V., Perrin, A., Polovtseva, E. R., Richard, C. , Smith, M., Starikova, E., Sung, K., Tashkun, S., Tennyson, J., Toon, G. C., Tyuterev, V. and Wagner, G. (2013). The HITRAN2012 molecular spectroscopic database. Journal of Quantitative Spectroscopy and Radiative Transfer, 130, 4-50.
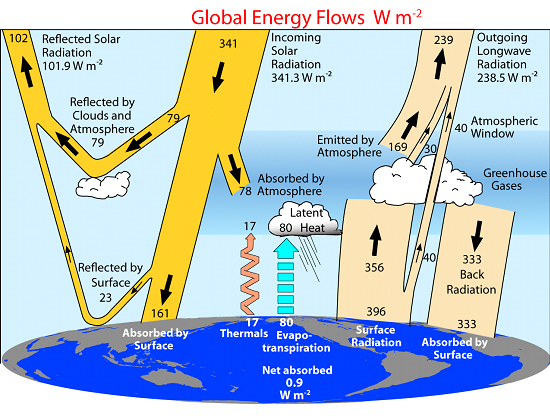
Trenberth, K. E., Fasullo, J. T., and Kiehl, J., (2009). Earth's global energy budget. Bulletin of the American Meteorological Society, 90, 311-323.
Wikle, C. K., Zammit-Mangion, A., and Cressie, N. (2019). Spatio-Temporal Statistics with R. Chapman and Hall/CRC Press, Boca Raton, FL.