| Rodney Nillsen's website
Home Page email: nillsen@uow.edu.au |
School Mathematics
|
|
|
It is quite clear that they never learned anything from me; the many fine discoveries to which they cling are of their own making. But to me and the god they owe their delivery -- Plato, Theaetetus |
The regular pentagon and the golden ratio 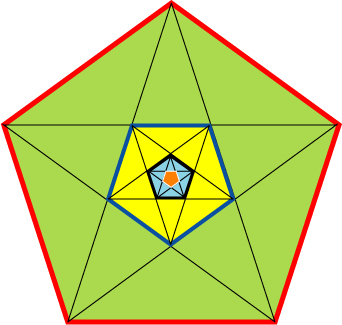
The picture shows a regular pentagon with red edges, where each edge has length $1$. Each vertex has lines drawn from the vertex to each of the other $4$ vertices. This produces, inside the original pentagon, a new regular pentagon -- the one with the blue edges. This process can now be repeated on the new pentagon, to produce another new regular pentagon. We can imagine this process continuing indefinitely, producing a sequence of regular pentagons, whose sides are getting smaller and smaller, in fact tending to zero. The upper horizontal line has length $(1+\sqrt{5})/2$, a number known as the golden ratio. Assume that this number is rational. Then, it can be shown from the above procedure that there is a positive number $r$ such that the lengths of the sides of the pentagons arising in the above process are all multiples of $r$. But this is impossible, as the lengths of the sides of the consecutive pentagons tend to zero as the process continues. Consequently, $(1+\sqrt{5})/2$ is not rational, and so $\sqrt{5}$ is not rational. Go to the golden ratio page for a detailed, elementary argument.
Convergence of p-series
This gives an accessible and calculus-free proof concerning the $p$-series, suitable for high school level.
See the following:
Rodney Nillsen: A proof that the series $\sum_{n=1}^{\infty}1/n^p$ is convergent for $p>1$,
The Mathematical Gazette 97 (2013), 273.
$ \textbf{Formulas for}\ \boldsymbol{\pi}$
A list of formulas for $\pi=3.14159265358...$ was prepared for Mathematics Teachers' Day at the University of Wollongong in June, 2007. One of these formulas, proved by
Srinvasa Ramanujan (1887-1920) is:
\[\frac{1}{\pi}=\frac{2\sqrt{2}}{9801}\sum_{n=0}^{\infty} \frac{(4n)!}{(n!)^4}\cdot \frac{26390n+1103}{396^{4n}}. \]
Another one of these formulas, proved in 1944, is:
\[\frac{22}{7}-\pi=\int_0^1\frac{x^4(1-x)^4}{1+x^2}\,dx.\]
You may read a list of the formulas here.
APPLICATIONS OF SCHOOL MATHEMATICS
In Australian public policy mathematics is generally seen as a secondary tool for data accumulation and associated statistical calculation and interpretation. A purpose in writing the material below was to illustrate and apply mathematics as a way of thinking, not simply as a set of rules for calculation, and as a potential tool for sustained investigation of public policy issues at the high school level. The work described below appeared in journals published by The Australian Association of Mathematics Teachers.
Public policy and quadratic functions 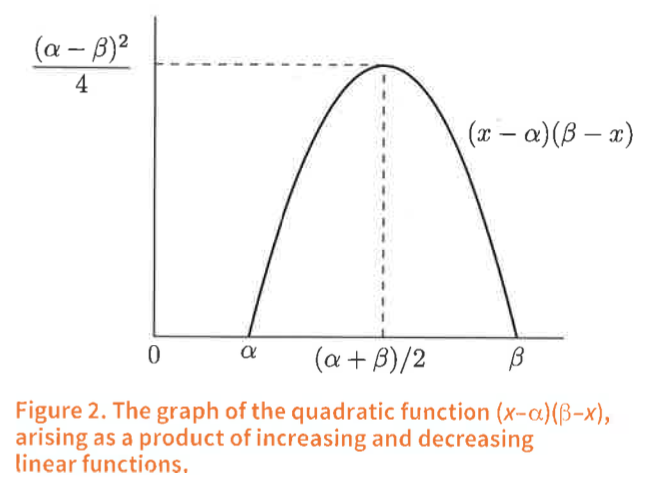
Let $\alpha$ and $\beta$ be two numbers with $\alpha<\beta$. Then the function $x-\alpha$ is increasing as $x$ increases, and the function $\beta-x$ is decreasing as $x$ increases. The product of these functions is $q(x)$ which equals
$(x-\alpha)\ (\beta-x)=-x^2+(\alpha +\beta)x-\alpha\beta.$
When we multiply an increasing and a decreasing function, we might wonder which function dominates, and for what values of $x$? The figure illustrates that $q(x)$ increases in $x$
when $\alpha< x< (\alpha+\beta)/2$ and that $q(x)$ decreases in $x$ when $\alpha< x< (\alpha+\beta)/2$, and that $q(x)$ decreases in $x$ when $(\alpha+\beta)/2< x< \beta$. Thus, the increasing function $x-\alpha$ dominates over $\beta-x$ for smaller values of $x$, while the opposite happens for larger values of $x$. There is a maximum value of $q(x)$ which occurs when $x-\alpha$ and $\beta-x$ are 'equally balanced' at $x=(\alpha+\beta)/2$. In this context of the conflicting tendencies of increase and decrease the 'optimal value' of $x$ for maximising $q$ is $(\alpha+\beta)/2$.
Now a large variety of policy issues can be thought of as optimising conflicting tendencies. Optimisation in the presence of conflicting tendencies, and the good and the bad about a policy options, is what permeates serious consideration of public policy and business decisions. The article (i) below considers the the above ideas in relation to optimising tax collection for a government, and for setting optimal pricing in retail businesses. I was trying also in the article to 'create' a language and way of thinking mathematically in words, to show how one can talk about mathematics in the same way as anything else. So, it has a high 'words to symbols ratio'.
See the following:
A comparison of two types of bank investments
Let us suppose a bank customer has $\$150,000$ to invest. The bank says it can offer an account where the bank pays interest compounded daily at 3% per annum. As an alternative, the bank offers also another account, where the
interest rate is 2.5% on the first $\$50,000$ and 3.5% on any amount in excess of $\$50,000$, where again the interest is compounded daily. The customer wishes to invest the $\$150,000$ for, say, five years. Which account should the customer choose? If the customer were prepared to wait for 10 years instead of five, would this make a difference to the account the customer should choose? Is there much difference between the two choices? Does a small change in an interest rate lead to a possibly large change in the outcome? More generally, in what ways do the interest rates and the other variables affect the answers to such questions?
In this paper, the above type of investment problem is investigated in terms of elementary algebra, recurrence relations, functions, and calculus at high school level. The problem comes down to understanding the behaviour of a function associated with the problem and, in particular, to finding the zero of the function. A wider purpose is not only to formulate the problem mathematically and to make necessary calculations, but to think on a wider front, and to seek insight and mathematical modes of thinking in relation to general investment strategy.
See the following :
Rodney Nillsen, A comparison of two types on bank investments, Australian Senior Mathematics Journal,31 (2017), 5-18.
Applications of school mathematics to resource allocation 
This work has its origins in a proposal from the West Report (1998) on higher education in Australia. The West Report considered possible changes to the monies allocated to universities on the basis of research. One method of doing this, and its implications, were discussed by David Phillips in an article in The Australian newspaper (July 1, 1998, page 41). The work mentioned below was carried out
in response to the David Phillips article, with the idea of using simple mathematics to clarify some of the issues. The talk and the papers below consider the issues as an abstract resource allocation problem. Using simple mathematics, the situation is analysed in somewhat more generality than in the article of Phillips, and the qualitative implications assessed. There is also a discussion of how, depending upon the circumstances, the parameters of the general procedure may be adjusted to avoid unacceptable outcomes, or to achieve ones considered desirable.
The specific problem in both the talk and the papers is to consider the implications when a method of resource allocation is changed by giving the criteria in the process different weightings from previously. The formulation of resource allocation problems in general mathematical terms potentially provides a greater understanding of the strengths and deficiencies of particular procedures and an appreciation of possible alternatives.
See the following:
(i) Rodney Nillsen An application of elementary functions to a resource allocation problem, Aust. Senior Math. Journal, 22 (2008), 29-35. (ii) Roderick West (committee chair), The West Report: Learning for Life, (1998). (iii) David Phillips, West's Quantum Mechanics, The Australian, 1st July 1998, p. 41. Phillips discusses some specific aspects. of the West Report. I am grateful to David Phillips for giving permission to make his article available on this site. (iv) Rodney Nillsen, An application of functions of the form (ax+b)/(cx+d) to modelling a problem of resource allocation, being slides of a talk given at the Mathematics Teachers' Day held at the University of Wollongong on June 27, 2006. Government funding of schools and taxpayer savings 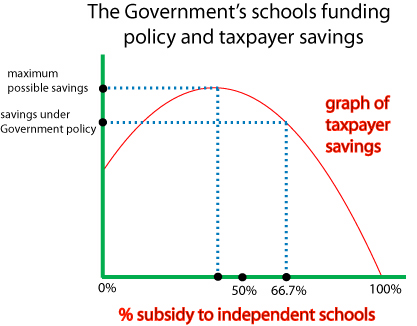
A controversial issue in Australia is the use of general taxpayer funds to provide subsidies for private or independent schools. (Note that in the UK these schools are called public schools). The Government often mentions that its policies save the taxpayer money, because subsidising pupils going to private schools is cheaper than paying the full cost for those pupils to go to a government school. In 2005 the then Minster, Brendan Nelson, stated that Government policy saved taxpayers $4 billion per year. A talk based on this issue was given to mathematics school teachers at the University of Wollongong in June 2005. The basic question addressed in the talk was: is the current Government subsidy at a level that maximises taxpayer savings? The accuracy of any conclusions depend upon the validity of the mathematical formulation of the problem, but the analysis is suggestive that the saving of public funds in this area of policy is an incidental effect of policy, rather than its main purpose. For example, under the assumptions , and if we further assume that 10% of pupils would go to independent schools even if there were no Government subsidy, the Government could save $1,252 million more than it does under current policy.
The analysis assumes a linear model for demand in relation to the subsidy, and this leads to a quadratic function for the savings in terms of the subsidy offered. However, high school mathematics discusses how to calculate the maximum value of a quadratic and where the maximum is attained. There are connections with the "Laffer curve", a mathematical curve (presumed quadratic) used in the USA under President Ronald Reagan as a reason for adjusting the tax rate.
See the following:
|