I’ve just arXived another revision of my paper on the PFAB algorithm: arXiv:1503.08066v3 [stat.CO]. It includes a rather elegant proof of the exact mean and variance of the sufficient statistic \(S(\mathbf{z})\) in the hottest state, when the inverse temperature \(\beta = 0\). The proof by my co-author Geoff Nicholls holds for any Potts model with first-order neighbours. That is, the nearest 4 neighbours in a 2D lattice (or 6 neighbours in 3D). For posterity, I present my rather clunkier proof below, which involves induction on dimension for a rectangular lattice.
The Potts (1952) model is an example of a Gibbs random field on a regular lattice, where each node \(y_i\) can take values in the set \(\{1, \dots, q\}\). The Ising model can be viewed as a special case, when \(q=2\). The size of the configuration space \(| \mathcal{Y} |\) is therefore \(q^n\), where \(n\) is the number of nodes. The dual lattice \(\mathcal{E}\) defines undirected edges between neighbouring nodes \(i \sim \ell\). If the nodes in a 2D lattice with \(c\) columns are indexed row-wise, the nearest (first-order) neighbours \(\partial(i)\) are \(\ell \in \{ i-1, i-c, i+c, i+1 \}\), except at the boundary. Nodes situated on the boundary of the domain have less than four neighbours. The total number of unique edges is thus \(\#\mathcal{E} = 2(n - \sqrt{n})\) for a square lattice, or \(2n - r - c\) if the lattice is rectangular.
The sufficient statistic of the Potts model is the sum of all like neighbour pairs: \[\begin{equation} S(\mathbf{y}) = \sum_{i \sim \ell \in \mathcal{E}} \delta(y_i, y_\ell) \end{equation}\] where \(\delta(a,b)\) is the Kronecker delta function, which equals 1 if \(a = b\) and equals 0 otherwise. \(S(\mathbf{y})\) ranges from 0, when all of the nodes form a chequerboard pattern, to \(\#\mathcal{E}\) when all of the nodes have the same value. The likelihood of the Potts model is thus: \[\begin{equation} p(\mathbf{y} \mid \beta) = \exp\{\beta S(\mathbf{y}) - \log \mathcal{C}(\beta)\} \end{equation}\] The normalising constant of the Potts model is intractable for any non-trivial lattice, since it requires a sum over the configuration space: \[\begin{equation} \label{eq:normConst} \mathcal{C}(\beta) = \sum_{\mathbf{y} \in \mathcal{Y}} \exp\{\beta S(\mathbf{y})\} \end{equation}\]When the inverse temperature \(\beta = 0\), \(p(\mathbf{y} \mid \beta=0)\) simplifies to \(\left(\sum_{\mathbf{y} \in \mathcal{Y}} \exp\{0\}\right)^{-1} = q^{-n}\), hence the labels \(y_i\) are independent and uniformly-distributed.
Theorem 1
The sum over configuration space of the sufficient statistic of the \(q\)-state Potts model on a rectangular 2D lattice is \(\sum_{\mathbf{y} \in \mathcal{Y}} \sum_{i \sim \ell \in \mathcal{E}} \delta(y_i,y_\ell) = q^{n-1} \#\mathcal{E}\).
Proof
For a \(q=2\) state Potts model on a lattice with \(n=4\) nodes and \(\#\mathcal{E} =4\) edges, \(\mathcal{Y}\) contains 16 possible configurations: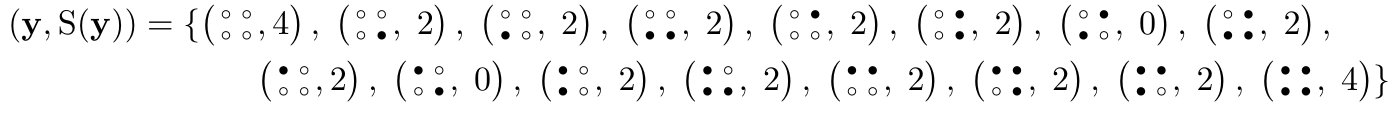 
\(\sum_{\mathbf{y} \in \mathcal{Y}} \mathrm{S}(\mathbf{y}) = 2 \times 4 + 12 \times 2 + 2 \times 0 = 32\). This can also be written as \(2^{3} \times 4 = 32\).
Now consider a rectangular lattice with \(r > 1\) rows and \(c > 1\) columns, so that \(n^\circ = r \times c\) and the dual lattice \(\#\mathcal{E}^\circ = 2 r \cdot c - r - c\). The size of the configuration space is \(|\mathcal{Y}^\circ| = q^{n^\circ}\). Assume that the sum over configuration space is equal to \(q^{n^\circ - 1} \#\mathcal{E}^\circ\). This sum can be decomposed into \((q^c)^r r(c-1)/q\) within each row, plus \((q^c)^r c(r-1)/q\) between rows.
If this lattice is extended by adding another row (or equivalently, another column), then \(n' = n^\circ + c\) (or otherwise, \(n' = n^\circ + r\)) and the dual lattice \(\#\mathcal{E}' = 2(n^\circ + c) - r - c - 1 = \#\mathcal{E}^\circ + 2c - 1\). The nodes in this new row can take \(q^c\) possible values, so the size of the configuration space is now \(|\mathcal{Y}'| = q^c q^{n^\circ} = q^{n'}\). \(\sum_{\mathbf{y} \in \mathcal{Y'}} S(\mathbf{y})\) will increase proportional to \(\frac{r+1}{r}q^c\) for the new row, plus \(\frac{r}{r-1}q^c\) for the connections with its adjacent row: \[\begin{eqnarray*} \sum_{\mathbf{y} \in \mathcal{Y'}} S(\mathbf{y}) &=& \frac{r+1}{r}q^c (q^c)^r \frac{r}{q}(c-1) + \frac{r}{r-1}q^c (q^c)^r \frac{c}{q}(r-1)\\ &=& \frac{r+1}{q} (q^c)^{r+1}(c-1) + \frac{r c}{q} (q^c)^{r+1} = q^{rc + c - 1} (2rc + c - r - 1) \\ &=& q^{n^\circ + c - 1} (\#\mathcal{E}^\circ + 2c - 1) = q^{n' - 1} \#\mathcal{E}' \end{eqnarray*}\]Q.E.D.
Theorem 2
The expectation of the \(q\)-state Potts model on a rectangular 2D lattice is \(\mathbb{E}_{\mathbf{y} | \beta = 0}[\mathrm{S}(\mathbf{y})] = \#\mathcal{E}/q\) when the inverse temperature \(\beta = 0\).
Proof
The proof follows from Theorem 1 by noting that \(p(\mathbf{y} | \beta = 0) = q^{-n}\) and hence: \[\begin{eqnarray*} \mathbb{E}_{\mathbf{y} | \beta = 0}[\mathrm{S}(\mathbf{y})] &=& \sum_{\mathbf{y} \in \mathcal{Y}} S(\mathbf{y}) \;p(\mathbf{y} \mid \beta = 0) \\ &=& q^{n-1} \#\mathcal{E} \;q^{-n} = \frac{\#\mathcal{E}}{q} \end{eqnarray*}\]Q.E.D.
Theorem 3
The sum over configuration space of the square of the sufficient statistic of the \(q\)-state Potts model on a rectangular 2D lattice is \[\begin{equation*} \sum_{\mathbf{y} \in \mathcal{Y}} \mathrm{S}(\mathbf{y})^2 = q^n \#\mathcal{E} \left(q^{-2}\#\mathcal{E} + q^{-1}(1 - q^{-1})\right). \end{equation*}\]
Proof
For a \(q=2\) state Potts model on a lattice with \(n=4\) nodes and \(\#\mathcal{E} =4\) edges, \(\sum_{\mathbf{y} \in \mathcal{Y}} \mathrm{S}(\mathbf{y})^2 = 2 \times 4^2 + 12 \times 2^2 + 2 \times 0^2 = 80\). This can also be written as \(2^4 \times 4 (4/2^2 + 0.5(1 - 0.5)) = 2^6(1 + 0.25) = 80\).
Now assume for a rectangular lattice with \(r>1\) rows and \(c>1\) columns that \[\begin{equation*} \sum_{\mathbf{y} \in \mathcal{Y}^\circ} \mathrm{S}(\mathbf{y})^2 = q^{rc - 2} (2rc - r - c)^2 + q^{rc - 1}\left(1 - \frac{1}{q}\right)(2rc - r - c). \end{equation*}\] This can be decomposed into \(\left( (q^c)^r r(c-1)/q + (q^c)^r c(r-1)/q \right)^2 + (q^c)^r (1 - q^{-1}) (2rc - r - c)/q\). If we extend the lattice by adding another row, then \[\begin{eqnarray*} \sum_{\mathbf{y} \in \mathcal{Y}'} \mathrm{S}(\mathbf{y})^2 &=& \left( \frac{r+1}{q} (q^c)^{r+1} (c-1) + \frac{rc}{q}(q^c)^{r+1} \right)^2 + (q^c)^{r+1} \frac{(1 - q^{-1})(2rc - r + c - 1)}{q}\\ &=& \left( q^{n^\circ + c - 1} (\#\mathcal{E}^\circ + 2c - 1) \right)^2 + q^{n^\circ + c - 1} \left(1 - q^{-1}\right) (\#\mathcal{E}^\circ + 2c - 1)\\ &=& \left( q^{n' - 1} \#\mathcal{E}' \right)^2 + q^{n' - 1} \left(1 - q^{-1}\right) \#\mathcal{E}' \\ &=& q^{n'} \#\mathcal{E}' \left(q^{-2}\#\mathcal{E}' + q^{-1}(1 - q^{-1})\right) \end{eqnarray*}\]Q.E.D.
Theorem 4
The variance of the \(q\)-state Potts model on a rectangular 2D lattice is \(\mathbb{V}_{\mathbf{y} | \beta = 0}[\mathrm{S}(\mathbf{y})] = \mathcal{I}(0) = \#\mathcal{E} q^{-1} (1 - q^{-1})\) when the inverse temperature \(\beta = 0\).
Proof
The proof follows from Theorems 1 and 3: \[\begin{eqnarray*} \mathbb{V}_{\mathbf{y} | \beta = 0}[\mathrm{S}(\mathbf{y})] &=& \mathbb{E}_{\mathbf{y} | \beta = 0}[\mathrm{S}(\mathbf{y})^2] - \mathbb{E}_{\mathbf{y} | \beta = 0}[\mathrm{S}(\mathbf{y})]^2\\ &=& \sum_{\mathbf{y} \in \mathcal{Y}} S(\mathbf{y})^2 \;p(\mathbf{y} \mid \beta = 0) - \left(\frac{\#\mathcal{E}}{q}\right)^2\\ &=& q^n \#\mathcal{E} \left(q^{-2}\#\mathcal{E} + q^{-1}(1 - q^{-1})\right) q^{-n} - \frac{\#\mathcal{E}^2}{q^2}\\ &=& \frac{\#\mathcal{E}^2}{q^2} + \#\mathcal{E} q^{-1} (1 - q^{-1}) - \frac{\#\mathcal{E}^2}{q^2} = \#\mathcal{E} q^{-1} (1 - q^{-1}) \end{eqnarray*}\]Q.E.D.