Professor and Former Head, Department of Computer Science. Director, Centre for Computer Security Research, University of Wollongong.
One hundred years ago, in 1893, Jacques Hadamard [21] found square matrices of orders 12 and 20, with entries +1, which had all their rows (and columns) orthogonal. These matrices, X = (xij), satisfied the equality of the following inequality 2 <= IIi=1n Sumj=1n |xij|2 and had maximal determinant. Hadamard actually asked the question of matrices with entries on the unit disc but his name has become associated with the real matrices.
Hadamard was not the first to study these matrices for J.J. Sylvester in 1867 in his seminal paper ``Thoughts on inverse orthogonal matrices, simultaneous sign-successions and tessellated pavements in two or more colours with application to Newton's rule, ornamental tile work and the theory of numbers'' [55] had found such matrices for all orders which are powers of two. Nevertheless, Hadamard showed matrices with elements +1 and maximal determinant could exist for all orders 1, 2, and 4t and so the Hadamard conjecture ``that there exists an Hadamard matrix, or square matrix with every element +1 and all row (column) vectors orthogonal'' came from here. The survey by J. Seberry and M. Yamada [51] indicates the progress that has been made in the past 100 years.
Hadamard's inequality applies to matrices from the unit circle and matrices
with entries +1, +i and pairwise orthogonal rows (and columns)
are called complex Hadamard matrices (note the scalar product is
ibi* for complex numbers).
These matrices were first studied
by R.J. Turyn [58]. We believe complex Hadamard matrices exist
for every order n
In the 1960's the U.S. Jet Propulsion Laboratories (JPL) was working toward building the Mariner and Voyager space probes to visit Mars and the other planets of the solar system. Those of us who saw early black and white pictures of the back of the moon remember that whole lines were missing. The first black and white television pictures from the first landing on the moon were extremely poor quality. How many of us remember that the recent fly-by of Neptune was from a space probe launched in the seventies? We take the high quality colour pictures of Jupiter, Saturn, Uranus, Neptune and their moons for granted.
In brief, these high quality colour pictures are taken by using three black and white pictures taken in turn through red, green and blue filters. Each picture is then considered as a thousand by a thousand matrix of black and white pixels. Each picture is graded on a scale of, say, one to sixteen, according to its greyness. So white is one and black is sixteen. These grades are then used to choose a codeword in, say, an eight error correction code based on, say, the Hadamard matrix of order 32. The codeword is transmitted to Earth, error corrected, the three black and white pictures reconstructed and then a computer used to reconstruct the coloured pictures.
Hadamard matrices were used for these codewords for two reasons, first, error correction codes based on Hadamard matrices have maximal error correction capability for a given length of codeword and, second, the Hadamard matrices of powers of two are analogous to the Walsh functions, thus all the computer processing can be accomplished using additions (which are very fast and easy to implement in computer hardware) rather than multiplications (which are far slower).
It was S. W. Golomb, L Baumert and Marshall Hall Jr [5] working with JPL who sparked the interest in Hadamard matrices in the past thirty years. They pioneered the use of computing in the construction of Hadamard matrices, the existence of which is an NPC problem (or a problem which has computational resources exponential in the input to find the answer but easy to check the answer once it has been given).
Sylvester's original construction for Hadamard matrices is equivalent to finding Walsh functions [24] which are the discrete analogue of Fourier Series.
Just as any curve can be written as an infinite Fourier series
n an Sin nt + bn Cos ntthe curve can be written in terms of Walsh functions
n an sal(i,t) + bn cal(i,t) = Sumn cn wal(i,t).The hardest curve to model with Fourier series is the step function wal2(0,t) and errors lead to the Gibbes phenomenon. Similarly, the hardest curve to model with Walsh functions is the basic Sin 2(Pi)t or Cos 2(Pi)t curve. Still, we see that we can transform from one to another.
Many problems require Fourier transforms to be taken, but Fourier transforms require many multiplications which are slow and expensive to execute. On the other hand, the fast Walsh-Hadamard transform uses only additions and subtractions (addition of the complement) and so is extensively used, as the foundation of the Fast Fourier Transform, to transform power sequence spectrum density, band compression of television signals or facsimile signals or image processing.
Walsh functions are easy to extend to higher dimensions (and higher dimensional Hadamard matrices) to model surfaces in three and higher dimensions - Fourier series are more difficult to extend. Walsh-Hadamard transforms in higher dimensions are also effected using only additions (and subtractions).
Some of the of the first significant papers describing Walsh-Hadamard transforms in higher dimensions is J Hammer and J Seberry [23, 22].
In 1976 Jennifer Seberry Wallis in her classic paper ``On the existence of
Hadamard matrices'' [59] showed that ``given any odd natural
number q there exists
a 2 (q-3)] so that there is an Hadamard matrix of order 2tq (and hence for
all orders 2sq, s >= t). This was the first time a general bound had been given for all
orders of Hadamard matrices. Previous results had been more ad hoc.
To achieve this result she had to invent a whole new area of Discrete Mathematics
known as ''Orthogonal Designs". Her theorem is represented graphically in Figure 1.
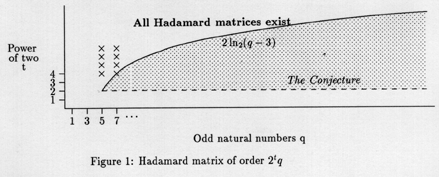
This result has been improved by R. W. Craigen and H. Kharaghani [11, 26]. In fact, as was shown in Seberry and Yamada [51], Hadamard matrices are known to exist, of order 22q, for most q < 3,000 (we have results up to 40,000 which are similar). In many other cases Hadamard matrices of order 23q or 24q exist. A quick look shows most of the very difficult cases are for q/ = 3 (mod 4).
Hadamard's original construction for Hadamard matrices is a ``multiplication theorem'' as it uses the fact that the Kronecker product of Hadamard matrices of orders 2am and 2bn is an Hadamard matrix of order 2{a+b}mn. Our graph shows we would like to reduce this power of two. In his book, Hadamard Matrices and their Applications, Agayan [4] shows how to multiply these Hadamard matrices to get an Hadamard matrix of order 2{a+b-1}mn (a result which lowers the curve in our graph except for q, a prime). This result has been extended by R. Craigen, Jennifer Seberry and Xian-Mo Zhang showed this astonishing ability to reduce the powers of two on multiplication could also be extended to the multiplication of four matrices at a time [10].
Paley's 1933 ``direct'' construction [41] which gives Hadamard matrices of order [II{i,j} (pi+1).[2.(qj+1)]], pi (prime power) = 3 (mod 4), qj (prime power) = 1 (mod 4) is extremely productive of Hadamard matrices but we note again the proliferation of powers of two as more products are taken. Paley also introduced matrices which, later when it became known that they gave the most efficient scheme for connecting a network for conference telephony, became known as conference matrices. To this day there are only four infinite classes of conference matrices known, Seberry pointed the way to the second of these classes and in [60], later Seberry and Whiteman [50] gave fourth and last discovered method.
Many people do not realize that in the same issue of the Journal of Mathematics and Physics as Paley's paper appears, J.A. Todd showed the equivalence of Hadamard matrices of order 4t and SBIBD(4t-1,2t-1,t-1). This family of SBIBD, its complementary family SBIBD(4t-1,2t,t) and the family SBIBD(4s2,2s2 + s, s2 + s) are called Hadamard designs. The latter family satisfies the constraint v=4(k - lambda) for v = 4s2, k=2ss + s and lambda =s2 + s which appears in some constructions (e.g. Shrikhande [54]). Hadamard designs have the maximum number of one's in their incidence matrices of all incidence matrices of SBIBD(v,k, lambda) (see Tsuzuku [57]). That Seberry [46] noted a special property of these matrices in "SBIBD(4k2, 2k2 + k, k2 + k) and Hadamard matrices of order 4k2 with maximal excess are equivalent", led to a number of authors finding many families of new designs in this special class [30, 47, 33].
In 1944 J. Williamson [62], who coined the name Hadamard determinants, first constructed what have come to be called Williamson matrices, or with a small set of conditions, Williamson type matrices. These matrices are used to replace the variables of a formally orthogonal matrix. We say Williamson type matrices are ``plugged in'' to the second matrix. Other matrices which can be ``plugged in'' to arrays of variables are called suitable matrices. Generally the arrays into which suitable matrices are plugged are orthogonal designs which have formally orthogonal rows (and columns) but may have variations such as Goethals-Seidel arrays, Wallis- Whiteman arrays, Spence arrays, generalized quaternion arrays, Agayan families, Kharaghani's methods, regular s-sets of regular matrices which give new matrices. This is an extremely prolific method of construction. Seberry and her students have made extensive use of computers to a mass data for relevant searches.
Another area which Seberry has popularized is the study of weighing matrices, which are square matrices, (W(n,k) = W with elements 0, + 1, which satisfy WWT = kI. These matrices are interesting because they tell us hold to design the most efficient experiments to weigh very small objects and design masks for diffraction gratings for spectroscopic analysis.
Seberry conjectured that if n = 0 (mod 4) there exists a W(n,k) for all k, 0 <= k <= n". This has led to an explosion of interest around the world with email collaboration between Greece, Israel, Japan, Australia, Canada, Taiwan, USA and Mexico.
Seberry and her co-authors have made many conjectures relating to weighing matrices, Hadamard matrices and orthogonal designs. The hierarchy of conjectures for weighing matrices and OD's is more straightforward. Settling the OD conjecture in Table 1 would settle the weighing matrix conjecture to its left.
----------------------------------------------------------------------
| Matrices | OD's |
----------------------------------------------------------------------
Strongest | Skew-weighing | OD (n;1,k) |
| Weighing W(n;k) n odd | |
| Weighing W(2n,k) n odd | OD (2n;a,b) n odd |
| Weighing W(4n,k) n odd | OD (4n;a,b,c,d) n odd |
Weakest | W(2sn,k), n odd, s >= 3 | OD(2sn;u1,u2,...,us) n odd |
----------------------------------------------------------------------
Table 1 : Weighing matrix and OD conjectures
Engineers concerned with finding the exact distance from their Earth base to the Moon, Venus and the other planets, or even to a moving aircraft,use radar signals which consist of sequences of binary entries, effectively 1 and -1. Unfortunately they have found that the type of single sequences they prefer to use, known as Barker sequences, apparently do not exist for lengths greater than 13.
A desire for longer usable sequences has prompted research engineers to consider sets of two or more binary and ternary sequences for these problems and others concerned with range, depth or information compression. Depending on the number of sequences and the alphabet of their description we have various sequences known as Golay, ternary pairs, Turyn, T-, base, normal, base, Yang and near-Yang sequences.
There has been an extensive search for Golay sequences but except for Turyn's result that these sequences exist for all lengths of the form 2a10b26c, where a,b and c are non-negative integers, all other results have proved negative. Recent theoretical work by Koukouvinos and Kounias [29], Koukouvinos, Kounias and Sotirakoglou [27] (* see final remark) and Eliahou, Kervaire and Saffari [16, 17] show that Golay sequences do not exist for n=2p where p has any prime factor equal to 3 (mod 4). This means the unresolved cases < 200 are n=74,82,106,116,122,130,136,146, 148,164,170,178,194.
Seberry and her student and colleague Genet Edmonson and M Anderson [15], were able to establish that all Turyn sequences of length <= 43 were known, the longest length being 15. Given these disappointing results the search shifted to other kinds of 4 complementary sequences Seberry and her student Joan Cooper [9] were able to find sequences of commuting variable which led to the entire new field of Orthogonal Designs.
Recently Seberry and her student Marc Gysin [19, 20] have applied the powerful theory of cyclotomy to search for 2-complementary and 4-complementary sequences, supplementary differences, Hadamard matrices, weighing matrices, statistical designs such as D-optimal and SBIBD [28, 31, 33, 47, 48, 34, 42]. Cyclotomy has been used since the fundamental paper of Bose in 1939 to find balanced incomplete block designs for medical and agricultural experiments. D. Dokovic has used a similar approach to search for specials kinds of Hadamard matrices and D-optimal designs with considerable success, optimal designs [31].
Using another method Seberry and her colleague C Koukouvinos were able to find the first infinite family of the statistical designs known as D-optimal designs [32].
Seberry has also pioneered the whole field of Bhaskar Rao Designs, which are now coming to the fore in relation to perfect hashing functions and cryptographic functions.
There are two types of cryptographic algorithms: private key and public key. Public key algorithms are thought to be very secure in practice but too slow for high rates of data flow desired. Public key methods can be used in a hybr- id system to transmit keys for use in private key encryption schemes which are needed to encrypt data at rates of megabytes per second.
Hadamard matrices and bent functions are used in the study of the design of S-boxes which are fundamental to the construction of cryptographically strong SPN algorithms (substitution-permutation-network)for private key cryptography.
Differential cryptanalysis and linear cryptanalysis, discovered by Biham and Shamir [6] and Matsui [36] respectively, are currently the most powerful cryptanalytic attacks against (secret-key) encryption ciphers (algorithms), especially against DES-like substitution-permutation ciphers. The attacks also apply to other cryptographic primitives such as one-way functions. Since the introduction of differential cryptanalysis, researchers have devoted consider- able effort to the design of S-boxes (substitution boxes) which are the core of many modern private key data encryption and hashing algorithms such as DES, LOKI, CASE, MD4, MD5 and HAVAL.
Seberry, as leader of the team which designed the LOKI family of encryption algorithms [7] and the HAVAL family [64] of hashing algorithms, encouraged the use of discrete mathematics and number theory in the design of these families. This is crucial as previously as many hashing algorithms have been compromised by mathematical insights into their structures. These families have now been made obsolete by new encryption and hashing standards. Seberry introduced the study of bent function to the academic researchers in Australia.
The strength of a cryptographic algorithm is primarily determined by that of the S-boxes employed by the algorithm and its key schedule which determines how to incorporate the secret key. In the recent past, a number of criteria for designing strong S-boxes have been identified by researchers in the field, including Gordon and Retkin [18], Webster and Tavares [61], Adams and Tavares [1, 2, 3], O'Connor [40], and Seberry, Zhang and Zheng [52]. Some of the criteria include high nonlinearity, the strict avalanche criterion (SAC), high order propagation, high nonlinear order and correlation immunity. While it is relatively easy to design S-boxes that satisfy some of these criteria, it has not been possible to have them satisfy all the criteria, since a few of the criteria seem to contradict each other. It is even more difficult to design S-boxes that balance the various criteria and resist the two most powerful known cryptanalytic attacks, differential cryptanalysis [6] and linear cryptanalysis [36].
Important ``cryptographic criteria'' that have to be taken into consideration include those for individual functions [3, 12, 37] and those for a set of functions. Criteria for individual functions include:
(i) being balanced, (ii) being highly nonlinear, (iii) satisfying the strict avalanche criterion (SAC), (iv) satisfying the propagation criterion, (v) having high nonlinear order (i.e. algebraic degree), (vi) satisfying the correlation immunity criterion, (vii) having no or small number of linear structures.
The above criteria are largely motivated by the two principles for security: ``confusion'' and ``diffusion''. The confusion means that the dependence of the key on the plaintext and ciphertext should be very complex, while the dif- fusion requires that each bit of plaintext and each bit of key influence each bit of ciphertext. For example, the nonlinearity is for confusion, while the SAC is for diffusion.
Only a few researchers have attempted to make a detailed study of the complex inter-relationships between the various cryptographic criteria.
In many cryptographic designs we not only require the individual component functions of the S-box to have good cryptographic properties but also consider correlations among these individual functions [2, 12, 14, 39, 56]. This is best shown by linear cryptanalysis which exploits low nonlinearity of linear combinations of the component functions of an S-box. Consequently, each nonzero linear combination of the components should satisfy a number of strict conditions.
Seberry and her colleagues X-M Zhang and Y Zheng [53] used group Hadamard matrices, which are closely related to Bhaskar Rao designs [45], and generalized Hadamard matrices [44] to obtain extremely secure cryptographic boolean functions.
To counter the differential attack, it has been realized that S-boxes should have good difference distribution tables. Based on early work in [2, 12, 14, 39, 56], Seberry and X-M Zhang identified the three principles for strong difference distribution tables of S-boxes which is captured by a measurement called robustness. So far no efficient method has been found to genera- te S-boxes having good difference distributions and also satisfying other criteria.
Seberry has made other significant contributions to privacy and security.
With her student and colleague M Miller [38], she introduced the concept of relative compromise of statistical databases. This gave a new and unfo- reseen method to compromise the confidentiality and privacy of information and is based on combinatorial designs.
She led the team which proposed beaconising networks [25] to provide authenti- cation services. The advantage of this method is that it avoids previous prot- ocol problems associated with replay attacks and provides an alternative to timestamping. She has studied a number of other scenarios (see for example [13]) involving the real problem of all networks, authentication, are you sure you are communicating with the party with whom you think you are communicating.